AlphaGeometry is as precise at solving geometry problems as an Olympiad gold medalist

AlphaGeometry is an AI system that solves elaborate geometry problems with an accuracy approaching that of a gold-medalist Olympian. It was recently introduced in a paper published in Nature and authored by a team of Google DeepMind and NYU researchers. AlphaGeometry was subjected to a benchmarking test composed of 30 geometry problems sourced from the International Mathematical Olympiad, managing to solve 25 problems within the IMO time limit. The previous state-of-the-art system, known as Wu's method, solved only 10 of them, while the Olympic gold medalist solved 25.9, on average.

Two salient hurdles to overcome when developing AI systems to solve complex mathematical problems are the models' lack of reasoning skills and a lack of digestible training data. AlphaGeometry manages to avoid both of them by using equally groundbreaking strategies: a neural language model complements a rule-bound deduction engine to find creative yet rigorous solutions to each of the problems, and the whole system was trained on a pool of 100 million unique examples which were synthetically generated using a custom method that does not depend on human-generated demonstrations.

When working together, the neural model and deduction engine have specific roles that contribute to different aspects of the problem-solving process. Olympiad geometry problems are often represented using diagrams that require additional constructs before a solution can be reached. The neural language model can quickly predict applicable constructs for solving a given problem by harnessing its pattern recognition capabilities and applying them to the vast corpus of data it was trained on. Including an additional construct enables the engine to perform further deductions that take the system closer to a solution. If no solution is found, the cycle is repeated, and the neural model can add further constructs until the problem is solved.

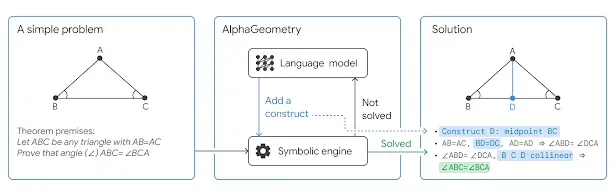
The synthetic data generation method was developed with how humans gather geometric knowledge using diagrams: using the existing diagram and previous mathematical knowledge, mathematicians uncover new relationships between geometric objects and novel facts about them. Then, they rely on the previously unknown data to sketch a solution to the problem. Similarly, AlphaGeometry's training began with the synthetic generation of one billion geometric diagrams, from which all the relations between their objects were derived using parallelized computing. Then, AlphaGeometry found all of the proofs that could be derived from the diagrams, noting whether additional constructs were needed and what they looked like, a process called symbolic deduction and traceback.

Finally, the pool was filtered so it wouldn't include redundant examples. This process yielded a 100-million pool of unique examples in varying difficulty levels. Additionally, nine million of these examples feature additional constructs. This aspect of the dataset is essential to AlphaGeometry's success: since it was given so many examples of how additional constructs aid in proof derivations, the language model was able to refine its construct-suggesting capabilities to a state-of-the-art level.

A final revolutionary aspect of AlphaGeometry is that its output is machine-verifiable but can also be read by humans. Previous AI solutions sometimes missed one or both of these characteristics, meaning that the generated solutions were not always correct or needed human checks. The readability of AlphaGeometry's output was confirmed by math coach and former gold medalist Evan Chen, who evaluated a selection of AlphaGeometry's solutions. He contrasted AlphaGeometry's method against a brute force system that could have solved the same problems using "pages and pages of tedious algebra calculation." Chen attributes the cleanliness and verifiability of AlphaGeometry's proofs to the fact that "[i]t uses classical geometry rules with angles and similar triangles just as students do."

The team behind AlphaGeometry recognizes that, in addition to being a groundbreaking development on its own, AlphaGeometry could also represent an essential step towards advanced general AI systems. For this reason, they decided to open-source the code and model, which can be found here.